使用R#语言求解线性规划问题

文章阅读目录大纲

估计阅读时长: 30 分钟

https://github.com/xieguigang/sciBASIC/

线性规划（Linear programming,简称LP）方法起源于20世纪40年代，由美国数学家乔治·丹齐格（George Dantzig）提出，并设计了著名的“单纯形法”。这种优化算法是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。通俗点的来讲，就是我们基于这一种数学优化技术，用于在一组线性约束条件下，求解线性目标函数的最大值或最小值（就是在“有限资源”和“一定规则”下，找到“最佳方案”的一种方法）。

生物信息学中的典型线性规划问题

在系统生物学领域内，有着一个非常经典的FBA（Flux Balance Analysis）方法进行代谢网络的数学建模分析。FBA方法是基于线性规划进行代谢网络最优化问题的求解。通过FBA分析，其可以让我们实现，例如如何在已知代谢网络（如细菌、细胞）中，预测各反应的代谢通量，从而解释或预测生物体在特定条件下的生长、产物合成等行为。

我们可以用如下所示的简单语言来描述这个代谢工程模型

决策变量：每个代谢反应的通量（流量）。
目标函数：最大化生物质（生长）或特定代谢产物产量。
约束条件：稳态假设下，每个代谢中间体的净通量为零（即质量守恒），并设定反应通量上下限。
数学形式：

其中S为化学计量矩阵，v为通量向量。

Illustration of genome-scale metabolic reconstruction and flux balance analysis.

a. Genome-scale metabolic reconstructions are built in two steps. First, several platforms exist for the generation of a gap-filled draft metabolic reconstruction based on genome annotations. Second, the draft reconstructions need to be refined based on known experimental and biochemical data from literature 7. Novel experiments can be performed on the organism and the reconstruction refined accordingly.

b. In flux balance analysis (FBA), the metabolic reconstruction containing n reactions and m metabolites is converted to a stoichiometric matrix S. FBA solves an optimization problem where an objective function Z is maximised or minimised. Z is formed by multiplying every reaction flux vi with a predetermined constant, ci, and adding the resulting values. FBA solves a steady state, Sv = 0. Every reaction i is bound by two values, an upper bound (ubi) and lower bound (lbi).

c. The solution space is defined by the mass balanced constraints imposed for the upper and lower bounds of each reaction in the metabolic reconstruction. Optimisation for a biological objective function (e.g. biomass production, ATP consumption, heme production, etc.) identifies an optimal flux within the solution space, whereas uniform sampling provides an unbiased characterisation by sampling candidate fluxes distributed in the solution space.

Creation and analysis of biochemical constraint-based models: the COBRA Toolbox v3.0 DOI:10.1038/s41596-018-0098-2

在这里我来为大家介绍一下在GCModeller软件包之中对FBA问题进行线性规划求解的计算引擎的开发。

线性规划问题描述

在线性规划数学模型中，一般我们能够找到决策变量很多个解。即有很多种方案，在这里我们以仅包含有两个变量的线性规划模型为例，将所有约束条件用图形绘出：

图中的彩色线段为约束条件，这些线段所围成的一个多边形为可行解。这个图中所示的变量只有[x1, x2]两个变量的线性规划问题。

对于上图所示的一个简单线性规划问题而言，一般会存在有以下几种解：

【可行解】凡满足所有约束条件的所有解称为可行解,它们对应可行方案。所有可行解的集合构成可行解域。即图中阴影部分。可行解域中的任何一点称为可行点，对应一个可行方案，这个点的坐标[x1, x2]构成一个列向量，称为可行向量。
【最优解】凡使得目标函数Z值达到最优(最大或最小)的可行解称为最优解。最优解一般情况下是唯一存在的，但在一些特殊的规划问题中，可能有无穷多个最优解或者不存在最优解。
【基本解】所有约束条件直线的交点对应的解称为基本解。
【基本可行解】可行解域边界上的约束条件直线的交点对应的解称为基本可行解，即上图中所有约束条件线段相交的点对应的解。它满足两个条件：其一是基本解，即约束条件直线的交点对应的解；其二是可行解，即满足所有的约束条件，在可行解域内。

从结构上看，线性规划数学模型包括目标函数、约束条件和变量非负约束三个部分。完整的表达式为：

单纯形法求解线性规划问题（Simplex Method）

单纯形法是1947年美国数学家丹捷格(G.B.Dantzig)提出的一种用于一般线性规划问题求解的方法。这种方法其主要的核心思想为从可行域的一个顶点出发，迭代到相邻更优顶点，直到最优。这种LP问题求解计算方法会比较适合于中小规模、精确解需求高的线性规划问题。单纯形法首先要做的就是把方程化为标准形式：

所有的变量都是非负数
所有的约束都是等式(非负限制除外)，且具有非负的右端项

在这里我们以一个简单实例来讲解单纯形法的计算机代码实现。假设我们有一个简单的线性规划问题，如下所示：

max z = 3x₁ + 2x₂ + 5x₃ + 4x₄ + x₅
s.t.
  2x₁ + 3x₂ +  x₃ + 2x₄ +  x₅ ≤ 10  (约束1)
   x₁ + 2x₂ + 3x₃ +  x₄ + 2x₅ ≤ 8   (约束2)
  3x₁ +  x₂ + 2x₃ + 3x₄ +  x₅ ≥ 5   (约束3)
   x₁ +  x₂ +  x₃ +  x₄ +  x₅ = 7   (约束4)
  2x₁ +  x₂ +  x₃ + 2x₄ + 3x₅ ≤ 9   (约束5)

问题标准化（Make Standard Form）

将不等式约束转化为等式约束，为单纯形法做准备。通过添加松弛变量（≤约束）或剩余变量（≥约束）使所有约束变为等式。例如，约束2x₁ + 3x₂ ≤ 10变为2x₁ + 3x₂ + s₁ = 10（s₁为松弛变量）。代码中addVariableAt方法动态添加变量，constraintTypes统一修改为"="。此步骤确保所有约束符合单纯形表的标准形式，是后续计算的基础。

Sub makeStandardForm()
    For i As Integer = 0 To constraintTypes.Length - 1
        If constraintTypes(i) <> "=" Then
            addVariableAt(i, If(constraintTypes(i) = "≥" OrElse constraintTypes(i) = ">=", -1, 1))
            constraintTypes(i) = "="
        End If
    Next
End Sub

针对上面的示例模型，在这里我们约束1/2/5添加松弛变量s₁,s₂,s₅（系数+1），约束3添加剩余变量s₃（系数-1），约束4不变。在这个函数的代码中makeStandardForm调用addVariableAt，constraintTypes全改为"="。

人工变量分配（Artificial Variable Assignments）

我们在这里为缺少初始基变量的约束添加人工变量。≥约束和=约束没有天然基变量，需人工变量构造初始可行基。例如，约束x₁ + x₂ = 7添加人工变量a₁变为x₁ + x₂ + a₁ = 7。代码通过检查约束类型和新增变量位置（originalVariableCount）确定需要人工变量的约束，返回索引列表。人工变量是两阶段法的关键，确保第一阶段有单位矩阵作为初始基。

''' <summary>
''' 根据约束类型和添加的变量系数判断是否需要人工变量
''' </summary>
''' <returns></returns>
Friend Function ArtificialVariableAssignments() As List(Of Integer)
    Dim assignments As New List(Of Integer)()
    Dim k As Integer = 0
    For j As Integer = 0 To constraintTypes.Length - 1
        ' 检查是否添加了松弛/剩余变量
        If constraintCoefficients(j).Count > originalVariableCount Then
            Dim lastCoeff As Double = constraintCoefficients(j).Last
            ' "≥"约束需要人工变量（系数为-1）
            If lastCoeff = -1 Then
                assignments.Add(originalVariableCount + k)
                k += 1
            Else ' "≤"约束不需要人工变量
                assignments.Add(-1)
            End If
        Else ' 原始等式约束需要人工变量
            assignments.Add(originalVariableCount + k)
            k += 1
        End If
    Next
    Return assignments
End Function

例如，在上面的实际的LPP模型例子中，约束3（≥）和约束4（=）需人工变量a₃,a₄。

第一阶段求解（Phase1）

在这一步中的主要目的式为了最小化人工变量之和，寻找原问题的可行解。目标函数替换为min w = Σaᵢ（aᵢ为人工变量）。例如，实例中目标变为min w = a₁ + a₂。代码保存原始目标函数后，设置人工变量系数为1，执行单纯形迭代。若最优解w=0，说明找到可行基；否则原问题无可行解。此阶段验证问题可行性，避免第二阶段无效计算。以上面所展示大的实际的LPP模型例子为例，我们在这里的目标改为min w = a₃ + a₄。迭代后若w=0，移除人工变量。

''' <summary>
''' 第一阶段：最小化人工变量之和
''' </summary>
Private Function Phase1(showProgress As Boolean, log As StringBuilder) As LPPSolution
    ' 保存原始目标函数
    Dim originalObj = lpp.objectiveFunctionCoefficients.ToArray()
    Dim originalValue = lpp.objectiveFunctionValue

    ' 设置第一阶段目标：最小化人工变量之和
    For i = 0 To lpp.objectiveFunctionCoefficients.Count - 1
        ' 只对人工变量设置系数为1，其他为0
        lpp.objectiveFunctionCoefficients(i) = If(IsArtificialVariable(i), 1, 0)
    Next
    lpp.objectiveFunctionValue = 0

    ' 初始化第一阶段基变量
    Dim basicVars = InitializePhase1BasicVariables()
    Dim artificialVarsList = GetArtificialVariablesList()

    log.AppendLine($"Phase 1: Initialized {basicVars.Count} basic variables")
    log.AppendLine($"Phase 1: Found {artificialVarsList.Count} artificial variables")

    ' 执行单纯形迭代
    Dim result = RunSimplexIteration(basicVars, artificialVarsList, log, showProgress)

    If result IsNot Nothing Then
        ' 恢复原始目标函数后再返回
        RestoreOriginalObjective(originalObj, originalValue)
        Return result
    End If

    ' 检查可行性
    If std.Abs(lpp.objectiveFunctionValue) > EPSILON Then
        RestoreOriginalObjective(originalObj, originalValue)
        Return New LPPSolution("No feasible solution (phase 1 optimal value > 0)", log.ToString, 0)
    End If

    ' 恢复原始目标函数
    RestoreOriginalObjective(originalObj, originalValue)
    log.AppendLine("Phase 1 completed successfully")

    Return Nothing
End Function

第二阶段求解（Phase2）

这个阶段的代码主要是移除人工变量后求解原目标函数。恢复原始目标（如max z = 3x₁ + 2x₂ + ...），以第一阶段得到的可行基继续迭代。代码中RemoveArtificialVariables删除人工变量，GetCurrentBasicVariables获取当前基变量，然后运行单纯形迭代直至最优。例如，实例中从第一阶段基出发，优化原始目标函数值。此阶段专注于原问题的最优解搜索。同样的，针对上面所展示的实际的LPP模型，算法代码在这里恢复目标max z，用可行基继续迭代。

''' <summary>
''' 第二阶段：求解原问题
''' </summary>
Private Function Phase2(showProgress As Boolean, log As StringBuilder) As LPPSolution
    ' 重新计算目标函数行
    Dim basicVars = GetCurrentBasicVariables()
    For Each row In basicVars.Select(Function(v, i) New With {.var = v, .row = i})
        If row.var >= 0 Then
            Pivot(row.var, row.row)
        End If
    Next

    ' 执行单纯形迭代
    Return RunSimplexIteration(basicVars, New List(Of Integer), log, showProgress)
End Function

单纯形迭代（Run Simplex Iteration）

那，到这里这一步，就到了整个求解算法的核心部分了。我们在这个步骤中，通过入基/出基操作优化目标函数。选择检验数最优的变量入基（如ChooseEnteringVariable按目标函数类型选最大/最小系数），按最小比值规则选出基行（ChooseLeavingConstraint）。代码中Pivot方法执行行变换，将入基变量系数化为1，其他行对应系数清零。例如，迭代中若x₃入基、约束2出基，则旋转操作更新基变量。此步骤是单纯形法的核心，逐步逼近最优解。

''' <summary>
''' 核心单纯形迭代逻辑
''' </summary>
Private Function RunSimplexIteration(basicVars As List(Of Integer),
                            artificialVars As List(Of Integer),
                            log As StringBuilder,
                            showProgress As Boolean) As LPPSolution
    Dim iteration = 0
    Do While iteration < LPP.PIVOT_ITERATION_LIMIT
        ' 选择入基变量
        Dim enterVar = ChooseEnteringVariable(artificialVars)
        If enterVar = -1 Then Exit Do ' 最优解

        ' 选择出基约束
        Dim leaveRow = ChooseLeavingConstraint(enterVar)
        If leaveRow = -1 Then
            Return New LPPSolution("Unbounded solution detected", log.ToString, 0)
        End If

        ' 执行旋转
        Pivot(enterVar, leaveRow)
        basicVars(leaveRow) = enterVar
        log.AppendLine($"Pivot: x{enterVar + 1} in, row {leaveRow + 1} out")
        iteration += 1
    Loop

    If iteration = LPP.PIVOT_ITERATION_LIMIT Then
        Return New LPPSolution("Iteration limit exceeded", log.ToString, 0)
    End If

    Return Nothing
End Function

''' <summary>
''' 改进的旋转操作（增加数值稳定性检查）
''' </summary>
Public Sub Pivot(varIndex As Integer, constIndex As Integer)
    Dim pivotRow = lpp.constraintCoefficients(constIndex)
    Dim pivotElem = pivotRow(varIndex)

    ' 增强主元有效性检查
    If std.Abs(pivotElem) < EPSILON Then
        Throw New InvalidOperationException($"Pivot element too small ({pivotElem}) for numerical stability at variable {varIndex}, constraint {constIndex}")
    End If

    ' 使用更稳定的缩放因子计算
    Dim scale = 1.0 / pivotElem

    ' 应用缩放时避免累积误差
    For i = 0 To pivotRow.Count - 1
        pivotRow(i) = pivotRow(i) * scale
    Next
    lpp.constraintRightHandSides(constIndex) = lpp.constraintRightHandSides(constIndex) * scale

    ' 改进的消去过程，减少数值误差
    For j = 0 To lpp.constraintCoefficients.Length - 1
        If j <> constIndex Then
            Dim row = lpp.constraintCoefficients(j)
            Dim factor = row(varIndex)
            If std.Abs(factor) > EPSILON Then
                For i = 0 To row.Count - 1
                    row(i) = row(i) - factor * pivotRow(i)
                Next
                lpp.constraintRightHandSides(j) = lpp.constraintRightHandSides(j) - factor * lpp.constraintRightHandSides(constIndex)
            End If
        End If
    Next

    ' 更新目标函数系数
    Dim objCoeff = lpp.objectiveFunctionCoefficients(varIndex)
    If std.Abs(objCoeff) > EPSILON Then
        For i = 0 To lpp.objectiveFunctionCoefficients.Count - 1
            lpp.objectiveFunctionCoefficients(i) = lpp.objectiveFunctionCoefficients(i) - objCoeff * pivotRow(i)
        Next
        lpp.objectiveFunctionValue = lpp.objectiveFunctionValue + objCoeff * lpp.constraintRightHandSides(constIndex)
    End If
    lpp.objectiveFunctionCoefficients(varIndex) = 0
End Sub

''' <summary>
''' 获取当前基变量（改进的数值稳定性版本）
''' </summary>
Private Function GetCurrentBasicVariables() As List(Of Integer)
    Dim basicVars As New List(Of Integer)
    Dim variableCount = lpp.objectiveFunctionCoefficients.Count

    ' 为每个约束行找到基变量
    For rowIndex = 0 To lpp.constraintCoefficients.Length - 1
        Dim row = lpp.constraintCoefficients(rowIndex)
        Dim candidateVar = -1
        Dim maxCoeff = 0.0

        ' 寻找该行中系数最大的变量（更稳定的识别方法）
        For varIndex = 0 To variableCount - 1
            Dim coeff = std.Abs(row(varIndex))
            If coeff > EPSILON AndAlso coeff > maxCoeff Then
                ' 检查该变量是否可能成为基变量
                If IsPotentialBasicVariable(varIndex, rowIndex) Then
                    candidateVar = varIndex
                    maxCoeff = coeff
                End If
            End If
        Next

        basicVars.Add(candidateVar)
    Next

    Return basicVars
End Function

''' <summary>
''' 检查变量是否可能成为基变量
''' </summary>
Private Function IsPotentialBasicVariable(varIndex As Integer, currentRow As Integer) As Boolean
    ' 检查该变量在其他行中的系数是否足够小
    For rowIndex = 0 To lpp.constraintCoefficients.Length - 1
        If rowIndex <> currentRow Then
            Dim coeff = std.Abs(lpp.constraintCoefficients(rowIndex)(varIndex))
            If coeff > EPSILON Then
                Return False
            End If
        End If
    Next

    ' 检查在当前行中的系数不为零
    Return std.Abs(lpp.constraintCoefficients(currentRow)(varIndex)) > EPSILON
End Function

''' <summary>
''' 选择入基变量（改进检验数计算）
''' </summary>
Private Function ChooseEnteringVariable(artificialVars As List(Of Integer)) As Integer
    Dim direction = If(lpp.objectiveFunctionType = OptimizationType.MAX, -1, 1)
    Dim bestVar = -1
    Dim bestValue = 0.0

    For i = 0 To lpp.objectiveFunctionCoefficients.Count - 1
        If Not artificialVars.Contains(i) Then
            Dim rc = direction * lpp.objectiveFunctionCoefficients(i)
            If rc < bestValue - EPSILON Then
                bestValue = rc
                bestVar = i
            End If
        End If
    Next

    Return bestVar
End Function

''' <summary>
''' 选择出基约束（改进最小比值规则）
''' </summary>
Private Function ChooseLeavingConstraint(enterVar As Integer) As Integer
    Dim minRatio = Double.PositiveInfinity
    Dim minRow = -1

    For j = 0 To lpp.constraintRightHandSides.Length - 1
        Dim coeff = lpp.constraintCoefficients(j)(enterVar)
        If coeff > EPSILON Then
            Dim ratio = lpp.constraintRightHandSides(j) / coeff
            If ratio < minRatio - EPSILON OrElse (std.Abs(ratio - minRatio) < EPSILON AndAlso j < minRow) Then
                minRatio = ratio
                minRow = j
            End If
        End If
    Next

    Return minRow
End Function

同样的，以上面所展示的这个简单的LPP模型为例。我们在处理算法计算的过程中，对于这个LPP计算模型，若x₃入基（检验数最优），约束2出基（最小比值8/3），执行Pivot(2,1)（索引从0起）。在代码中的Pivot方法会更新系数矩阵，使x₃系数在约束2为1，其他行清零。上面所描述的代码执行过程，在结束了Phase2阶段的运行后，我们就可以得到目标LPP问题的解了。

单纯形迭代过程详细的数学算法原理

在上面所展示的代码中 RunSimplexIteration 和 Pivot 这两个函数是单纯形法求解器的引擎，前者是决策中心，负责制定每一步的移动策略；后者是执行者，负责完成代数变换以实现该策略。具体的来讲，就是在线性规划中，单纯形法的核心思想是从一个基本可行解出发，沿着可行域的顶点进行迭代，每次迭代都移动到一个能使目标函数值更优的相邻顶点，直到找到最优解或判定问题无界。RunSimplexIteration 函数完美地体现了这一迭代流程，而 Pivot 函数则实现了从一个顶点到另一个顶点的代数转换。

RunSimplexIteration 函数是单纯形算法的主循环控制器。它的数学目标是在当前的基本可行解基础上，判断是否已经达到最优，或者选择下一个更有潜力的顶点进行移动。这个过程遵循严格的数学准则，主要包括最优性检验和方向选择。这个计算函数的实现逻辑与数学原理如下：

循环与终止条件：函数通过一个 Do While 循环驱动迭代。循环的终止条件有两个数学依据：
- 达到最优解：当找不到任何一个可以改善目标函数值的入基变量时，迭代停止。这在代码中通过 ChooseEnteringVariable 返回 -1 来实现。
- 达到迭代上限：PIVOT_ITERATION_LIMIT 是一个工程上的安全措施，防止因数值问题或逻辑错误导致的无限循环，理论上单纯形法应在有限步内收敛。
选择入基变量：ChooseEnteringVariable 函数执行的是最优性检验。
- 数学原理：在单纯形表中，每个非基变量都有一个对应的检验数（Reduced Cost），通常表示为 σ_j = c_j - z_j，其中 c_j 是目标函数中该变量的系数，z_j 是将该变量引入基所需付出的“机会成本”。
- 对于最大化问题，如果所有非基变量的检验数 σ_j ≤ 0，则当前解已是最优，因为引入任何非基变量（使其值从0变为正）都不会增加目标函数值。如果存在 σ_k > 0，则将 x_k 引入基可以改善目标函数值。我们通常选择检验数最大的那个变量 x_k 作为入基变量，因为它能带来最快的单位改善。
- 对于最小化问题，规则相反，当所有 σ_j ≥ 0 时达到最优，选择 σ_k < 0 的变量入基。
- 代码实现：代码中 lpp.objectiveFunctionCoefficients 数组在每次旋转后都存储了当前的检验数。direction 变量巧妙地统一了最大化（direction = -1）和最小化（direction = 1）的判断逻辑。函数遍历所有非人工变量，寻找使 direction * lpp.objectiveFunctionCoefficients(i) 最小（即最负）的变量，这等价于寻找最有改善潜力的变量。
选择出基约束：ChooseLeavingConstraint 函数执行的是可行性检验，即著名的最小比值规则。
- 数学原理：当选定入基变量 x_k 后，我们需要确定它应该替换掉哪个当前的基变量。我们增加 x_k 的值，同时其他非基变量保持为0。基变量的值会根据约束方程 x_B = b - A_k x_k 发生变化（其中 x_B 是基变量向量，b 是右端项向量，A_k 是约束矩阵中 x_k 对应的列）。为了保持解的可行性，所有基变量的值必须非负：b_i - a_ik x_k ≥ 0。
- 对于 a_ik > 0 的约束，我们得到 x_k ≤ b_i / a_ik。为了使所有基变量都保持非负，x_k 的最大增量不能超过所有这些比值的最小值。这个最小比值对应的约束 i 就是出基约束，因为它的基变量会最先随着 x_k 的增加而变为0。
- 如果所有 a_ik ≤ 0，这意味着 x_k 可以无限增大而不会违反任何约束，目标函数值可以无限改善，因此问题无界。
- 代码实现：代码遍历所有约束，计算 lpp.constraintRightHandSides(j) / coeff（即 b_i / a_ik），但仅当 coeff > EPSILON（即 a_ik > 0）时才考虑。它跟踪最小的 minRatio 及其对应的行号 minRow。如果始终找不到 coeff > 0 的行，则返回 -1，表示无界解。
执行旋转：一旦确定了入基变量 x_k 和出基行 i，就调用 Pivot(k, i) 来完成基变换。这是从一个顶点移动到另一个顶点的具体操作。

Pivot 函数是单纯形法的计算核心，它执行的是高斯-若尔当消元法的一个步骤。其数学目标是：将线性方程组（包括目标函数）进行等价变换，使得新的基变量在约束矩阵中形成一个单位矩阵，从而可以直接从右端项读出新的基本可行解。在这个函数值中，假设我们选定变量 x_k（列 varIndex）入基，替换第 i 个约束（行 constIndex）中的基变量。主元就是 a_ik。实现的函数逻辑和数学原理如下所示：

主元行归一化：
- 数学原理：为了使新的基变量 x_k 在其所在的行（第 i 行）的系数变为1，我们将整个第 i 行的方程两边同时除以主元 a_ik。
- 新的第 i 行：(Row_i) / a_ik → x_k + (a_i1/a_ik)x_1 + ... + (a_in/a_ik)x_n = b_i / a_ik
- 代码实现：代码计算 scale = 1.0 / pivotElem，然后遍历 pivotRow（即第 i 行）的所有元素，乘以 scale。同时，lpp.constraintRightHandSides(constIndex) 也被乘以 scale。EPSILON 检查确保了数值稳定性，避免除以一个接近零的数。
其他行消元：
- 数学原理：为了使 x_k 在其他所有行（j ≠ i）中的系数变为0，我们对每一行执行行变换。新的第 j 行 = 旧行 j - a_jk * (新的第 i 行)。
- 新的第 j 行：(Row_j) - a_jk (Row_i / a_ik) → ... + 0x_k + ...
- 代码实现：外层循环遍历所有其他行 j。factor = row(varIndex) 即 a_jk。如果 factor 不为零，内层循环执行 row(i) = row(i) - factor * pivotRow(i)，这正是上述公式的实现。右端项 lpp.constraintRightHandSides(j) 也进行同样的更新。
更新目标函数行：
- 数学原理：目标函数 Z 也必须用非基变量来表示。同样地，我们消去目标函数中 x_k 的项。新的目标函数行 = 旧目标函数行 - c_k * (新的第 i 行)，其中 c_k 是 x_k 当前的检验数。旋转后，x_k 成为基变量，其检验数必须变为0。
- 代码实现：objCoeff 即 c_k。代码对 lpp.objectiveFunctionCoefficients 数组执行与约束行相同的消元操作。lpp.objectiveFunctionValue 也被相应更新。最后，lpp.objectiveFunctionCoefficients(varIndex) = 0 显式地将新基变量的检验数设为0，符合其数学定义。

R#脚本实例

在R#的线性代数计算环境之中，存在着一个lpSolve的程序包用来求解线性规划问题。在lpSolve程序包之中，主要是使用一个名叫lp的函数进行问题求解。这个lp函数主要接受三个参数：目标函数的极值方向，目标方程表达式以及线性规划的约束条件。通过lpSolve程序包可以用一种很自然语言的方法进行数学问题求解。例如有如下的一段脚本进行线性规划问题的求解：

imports "lpSolve" from "Rlapack";

# max objective function
let obj = lpSolve::lp.max(15*x1 + 19*x2 + 14*x3 + 3*x4 + 10*x5 + 18*x6 + 11*x7 + 5*x8 + 20*x9 + 14*x10);
let subj_to = lpSolve::subject_to(
     6*x1 + 3*x2 +  3*x3 + 10*x4 +  1*x5 +  7*x6 + 7*x7 + 6*x8 + 8*x9 + 9*x10 <= 100,
     9*x1 + 9*x2 +  8*x3 +  9*x4 +  7*x5 +  9*x6 + 5*x7 + 9*x8 + 2*x9 + 6*x10 <= 150,
    10*x1 + 9*x2 + 10*x3 +  3*x4 +  5*x5 +  9*x6 + 7*x7 + 2*x8 + 1*x9 + 5*x10 <= 200,
     5*x1 + 9*x2 +  7*x3 +  4*x4 + 10*x5 + 10*x6 + 5*x7 + 5*x8 + 9*x9 + 9*x10 <= 80
);
let lpp = lp(obj, subj_to);

str(lpp$solution);

print("objective value:");
print(lpp$objective);

# List of 10
#  $ x1  : num  16
#  $ x2  : num 0
#  $ x3  : num 0
#  $ x4  : num 0
#  $ x5  : num 0
#  $ x6  : num 0
#  $ x7  : num 0
#  $ x8  : num 0
#  $ x9  : num 0
#  $ x10 : num 0
#
# [1] "objective value:"
# [1]  240

Author
Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Attachments

linear-programming-example • 22 kB • 571 click
2021年8月11日
chi-graph-white-long • 24 kB • 501 click
2021年8月12日
Linear_Programming_Feasible_Region • 11 kB • 512 click
2021年8月12日
standard-canonical-form-of-an-lp-model-l • 45 kB • 493 click
2021年8月12日
Illustration-of-genome-scale-metabolic-reconstruction-and-flux-balance-analysis-a • 91 kB • 496 click
2021年8月12日

Illustration of genome-scale metabolic reconstruction and flux balance analysis
LPP_example • 807 kB • 508 click
2021年8月12日
v2-5dec0ea6987da4d18541ac96426ee57f_r • 25 kB • 489 click
2021年8月12日
v2-fd04eee1ae5c6b449c1a5dae63fa0c33_720w • 27 kB • 468 click
2021年8月12日
v2-9190a1cb7ca41650fc71eb27be494669_720w • 29 kB • 518 click
2021年8月12日
v2-d6285cf1ab3c125f0ff13592931ced44_720w • 26 kB • 494 click
2021年8月12日
FBA-lpp • 6 kB • 10 click
2025年12月3日
lpp-model • 28 kB • 9 click
2025年12月3日

打赏赞(4)

algorithm gem linear programming math metabolic network Operation Research R#VisualBasic

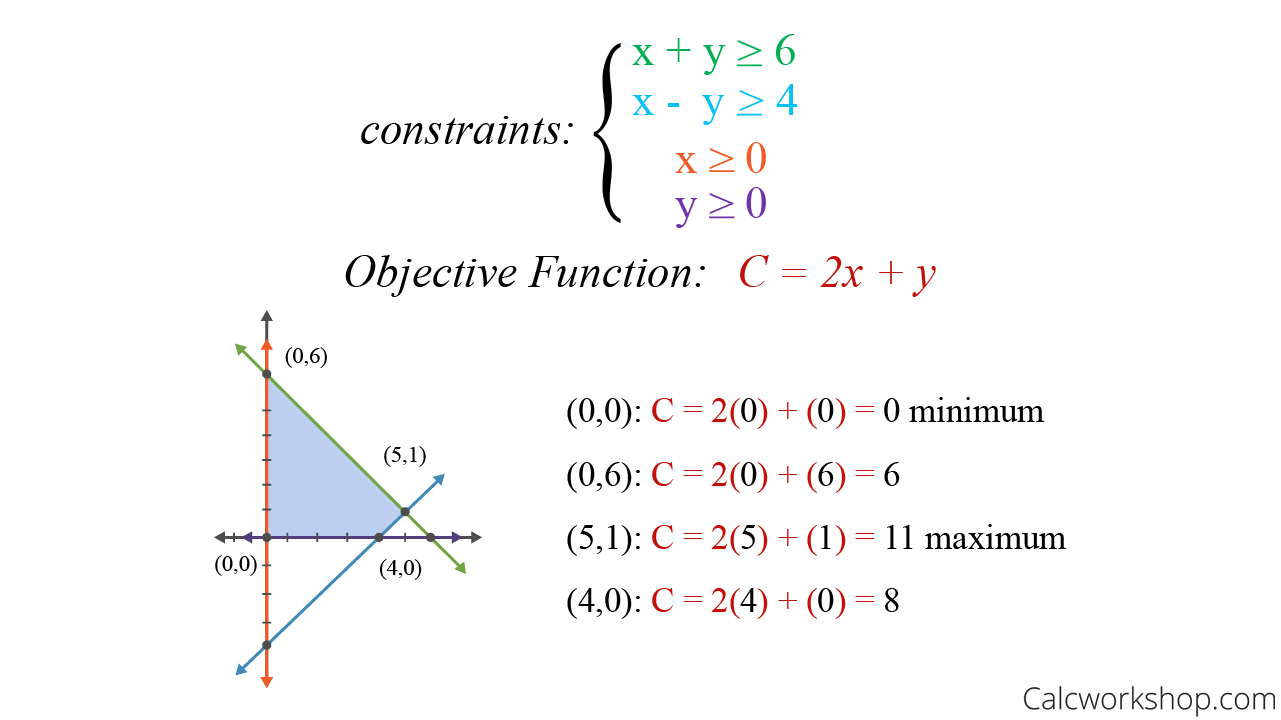
One response

记一次浅尝辄止的FBA代谢网络分析 – この中二病に爆焔を！ says:

2021年9月12日 at 3:07 PM

[…] 关于线性规划计算的原理，大家可以阅读博客文章《使用R#语言求解线性规划问题》，里面有比较详细的原理说明以及代码实现介绍。 […]

来自中国

Reply

https://github.com/xieguigang/sciBASIC/

生物信息学中的典型线性规划问题

线性规划问题描述

单纯形法求解线性规划问题（Simplex Method）

单纯形迭代过程详细的数学算法原理

R#脚本实例

Attachments

Related

One response

Leave a Reply Cancel reply

Recent Posts

Archives

博客文章

使用R#语言求解线性规划问题

https://github.com/xieguigang/sciBASIC/

生物信息学中的典型线性规划问题

线性规划问题描述

单纯形法求解线性规划问题（Simplex Method）

单纯形迭代过程详细的数学算法原理

R#脚本实例

Order by Date Name Attachments

Related

One response

Leave a Reply Cancel reply

Recent Posts

Archives

博客文章

Tags

Attachments